Massa-Veer Systemen
WB1643 Werktuigkundig Ontwerpproject 3
toegepaste mechanica
Massa-veer systemen vormen mooie modellen voor veel onderdelen van onze ontwerpen. Door een ingewikkeld ontwerp te vereenvoudigen naar een massa-veer systeem, kunnen we veel sneller de effecten van onze ontwerpkeuzes evalueren en bijstellen. Hier zullen drie toepassingen van massa-veer systemen analyseren en bespreken:
Valbestendigheid
Eigenfrequenties
Excitatie-respons
Valbestendigheid
Wat kunnen we doen om de effecten van een val te verminderen?
Mijn telefoon is, kort nadat ik een nieuw hoesje eromheen had gezet, gebarsten. Hoe kan het dat dit wel gebeurd met dit hoesje, maar niet met het originele hoesje?
De ninjabrugger gaat ongetwijfeld tijdens het testen een keer in “de lava” vallen. Is die dan meteen kapot of blijft die werken? Kunnen we daar op ontwerpen?
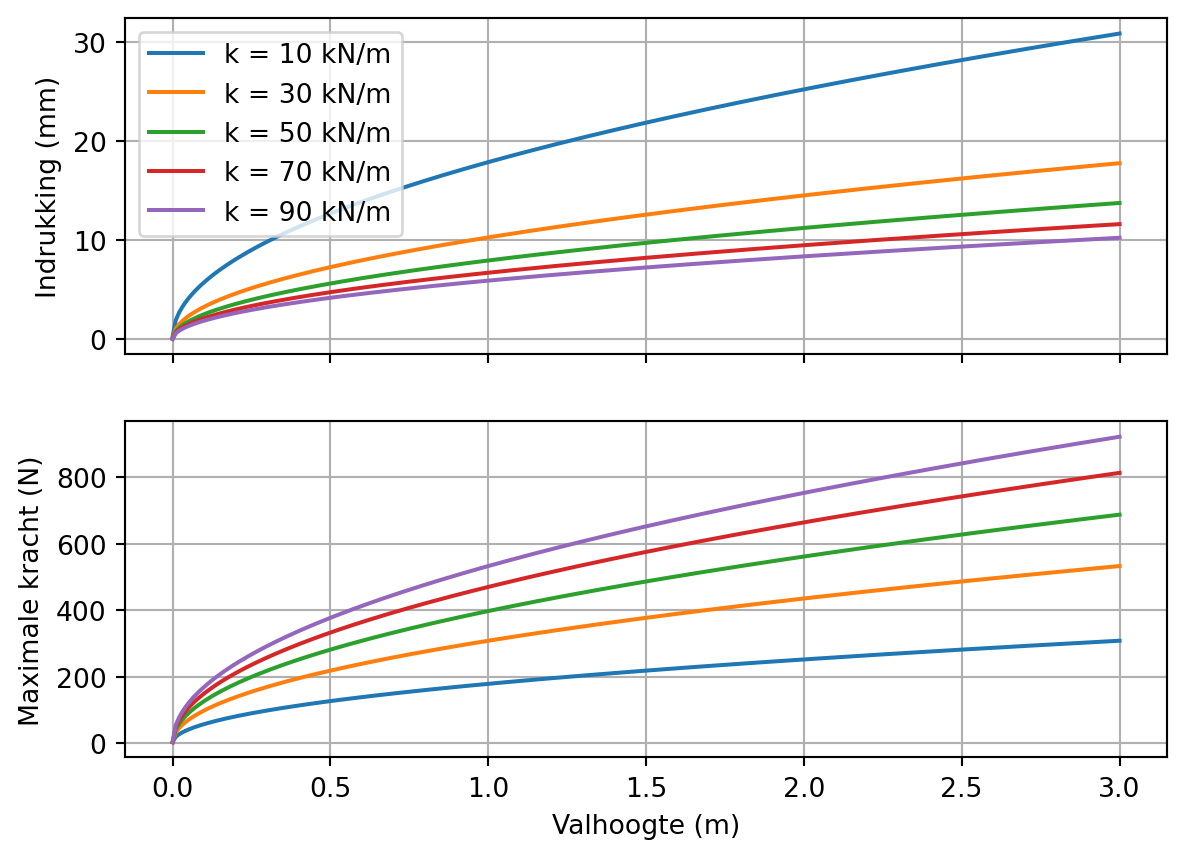
Als je van een tafel springt, veer je een beetje door je knieën. Zo verleng je de weg en wordt de landing comfortabeler. Wanneer je dit niet doet, voel je het in je knieën. De weg die je aflegt tijdens het landen maakt dus uit voor het effect van de val.
Bij vallen begin je met een energie \(E_h = mgh\). Bij het landen wordt die opgenomen door de grond. Hierbij levert de grond een arbeid \(\int F_n ds\), waarbij \(F_n\) de kracht van de grond op het object is.
Tijdens het landen zal het object wat indeuken (hopelijk hebben we hierop ontworpen). Dat vormt de weg waarover de kracht geïntegreerd wordt. Als we deze weg \(\delta\) noemen, krijgen we
\[\begin{aligned} mg(h + \delta) &= \int\limits_0^\delta F_n ds\\ &= \int\limits_0^\delta ks ds\\ &= \frac{k\delta^2}{2}\\ \delta^2 - 2\frac{mg}{k}\delta - 2\frac{mg}{k}h &= 0 \end{aligned}\]Deze is op te lossen met de ABC-formule om het volgende resultaat te krijgen:
\[ \delta = \left(1 \pm \sqrt{1 + \frac{2h}{\delta_\text{stat}}}\right)\delta_\text{stat} \]
Waar \(\delta_\text{stat}\) de statische indrukking is:
\[\delta_\text{stat} = \frac{mg}{k}\]
Dit geeft ons een versterkingsfactor voor de statische indrukking. Wanneer we de statische indrukking weten (vaak op basis van sterkteleer), kunnen we dus ook de indrukkingen bij vallen weten.
Dit geldt ook voor de spanningen. We gaan er immers bij het rekenen vanuit dat de verhoudingen lineair-elastisch zijn. Deze versterkingsfactor moet dus altijd kleiner zijn dan de veiligheidsfactor op de spanningen in ons materiaal.
Eigenfrequentie
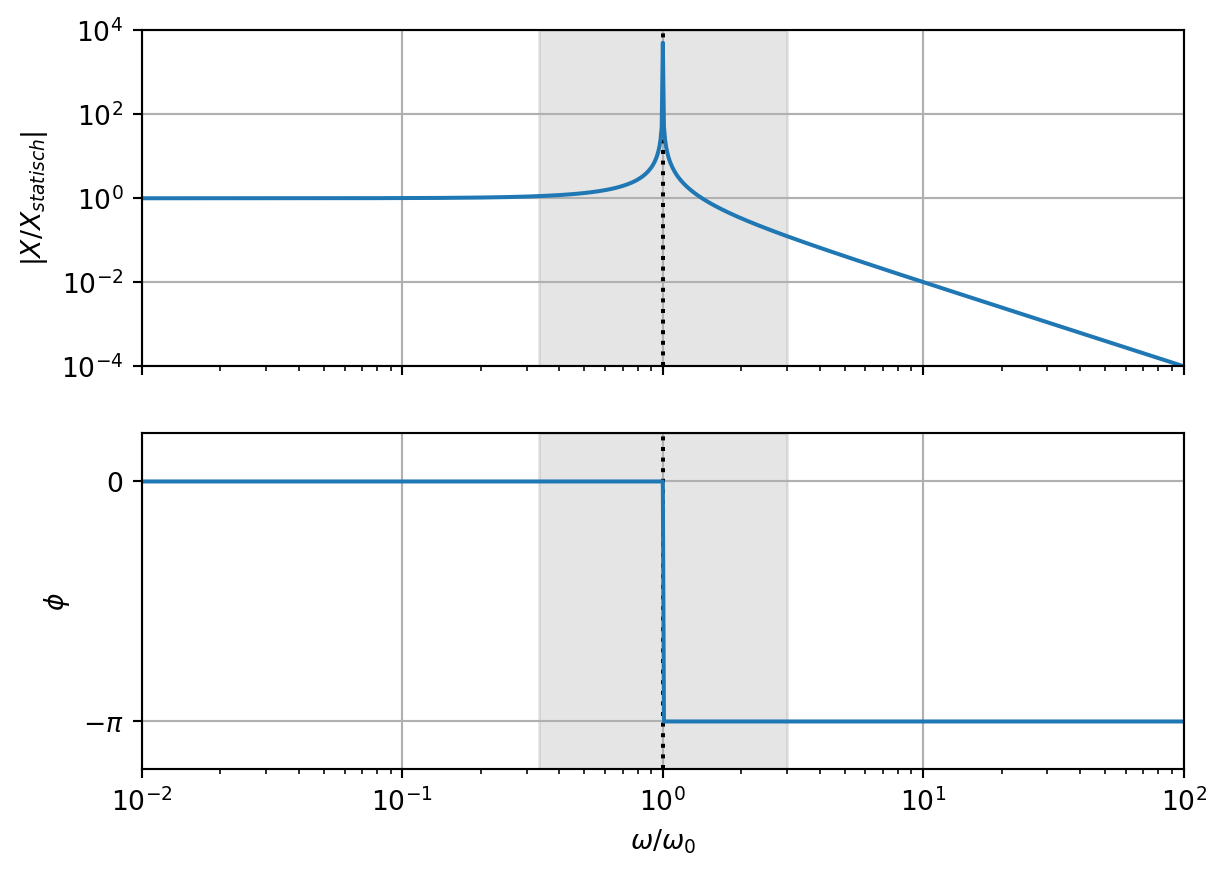
De eigenfrequentie is de natuurlijke frequentie van een massa-veer systeem. Wanneer het systeem aangeslagen wordt, zal het bij deze frequentie gaan trillen. Voor een beweging bij deze frequentie, is geen externe kracht nodig. Voor een ongedempt systeem zal de trilling dus altijd door blijven gaan.
De frequentie waarvoor dit geldt, is
\[ \omega_0 = \sqrt{\frac{k}{m}} \]
Met een veer kunnen we dus de massa van een object bepalen
Met een torsieslinger zou dit ook kunnen voor de traagheid
\[ \omega_0 = \sqrt{\frac{k_\phi}{I}} \]
Een massa aan het einde van een balk gedraagt zich ook als een massa-veer systeem. De stijfheid is dan de stijfheid van de balk. Die kunnen we afleiden uit de vergeetmenietjes:
\[\begin{aligned} \delta &= \frac{FL^3}{3EI}\\ k &= \frac{F}{\delta}\\ &= \frac{3EI}{L} \end{aligned}\]De eigenfrequentie wordt dan
\[ \omega_0 = \sqrt{\frac{k}{m}} = \sqrt{\frac{3EI}{mL^3}} \]
Let wel op dat we hier de massa van de balk zelf verwaarlozen. Wanneer dat niet kan, worden de vergelijkingen een stuk lastiger. De vorm waarin de balk trilt wordt dan belangrijk. Niet alle stukjes massa van de balk trillen immers met dezelfde amplitude. Door de Euler-Bernouilli vergelijkingen voor de balk numeriek op te lossen, kunnen we correctiefactoren vinden die de eigenfrequentie van de balk bepalen(Inman 2001). Wanneer er geen extra massa op de balk bevestigd is, worden de eigenfrequenties dan gegeven door:
Inman, D. J. 2001. Engineering Vibration. 2nd ed. Upper Saddle River, N.J.: Prentice Hall.
Ten opzichte van het massa-veer systeem is er dus een correctiefactor bijgekomen. Voor de eerste drie eigenmodes van een eenzijdig ingeklemde balk zijn deze
| n | \(\beta L\) |
|---|---|
| 1 | 1.875 |
| 2 | 4.694 |
| 3 | 7.855 |
Vaak is het makkelijk om dit uit te drukken in een “effectieve massa” voor de balk. Dit kunnen we doen door de formule om te schrijven. Voor de eerste eigenmodus vinden we dan
\[ m_\text{eff} = 0.2357 m \]
De eigenfrequentie wordt dan weer gegeven door
\[ \omega_0 = \sqrt{\frac{3EI}{m_\text{eff}L^3}} \]
Wanneer we nu een massa aan het einde van de balk toevoegen kunnen we die bij deze effectieve massa optellen.
Excitatierespons
Voor een aangedreven trilling maakt het veel uit of je dit in de buurt van de eigenfrequentie doet. In het boek van Cool (Cool e.a. 2023), wordt dit dan ook een scheidingsfrequentie genoemd. Voor een aandrijffrequentie die onder \(\frac{\omega_0}{3}\) zit, hoef je je niet zo’n zorgen te maken over de trillingen en kun je het systeem statisch benaderen. De uitwijking van de veer zal recht evenredig zijn met de kracht die erop gezet wordt.
Cool, Jan C., Gabriëlle J. M. Tuijthof, Giuseppe Radaelli, en Regine W. Vroom. 2023. Werktuigkundige Systemen. TU Delft OPEN Textbooks. TU Delft OPEN Textbooks. https://doi.org/10.59490/t.2023.006.
Bij een aandrijffrequentie boven \(3\omega_0\) worden juist de uitwijkingen minder belangrijk. De massa van het massa-veer systeem is dominant en werkt de opgelegde beweging tegen.
