Ontwerpen vanuit Fysische Principes

WB1642 Werktuigkundig Ontwerpproject 2

Auteurs

Affiliatie

Freek Broeren

TU Delft | Mechanical Engineering

Werner van de Sande

TU Delft | Mechanical Engineering

Figuur 1: Elon Musk over redeneren vanuit “First Principles”

Waar begin je met ontwerpen?

flowchart LR 
    A(Probleem) --> B[Analyse]
    B           --> C(Criteria)
    C           --> D[Synthese]
    D           --> E(Voorlopig Ontwerp)
    E           --> F[Simulatie]
    F           --> G(Verwachte Eigenschappen)
    G           --> H[Evaluatie]
    H           --> I(Waarde van het ontwerp)
    I           --> J{Beslissing}
    J           --> K(Aanvaardbaar Ontwerp)
    J         ----> B
    J         ----> D
    C         ----> H

Figuur 2: Basiscyclus van ontwerpen (Roozenburg en Eekels 1998)

In Figuur 2 zien we een overzicht van de stappen die we uitvoeren tijdens het ontwerpen. Zoals je daar ziet, beginnen we met een probleem en eindigen we (als het goed is) met een aanvaardbaar ontwerp. Om tot dit ontwerp te komen, moeten er vaak meerdere cycli doorlopen worden. Vandaar dat we vanaf de beslissing over de waarde van het ontwerp weer terug kunnen naar de synthese of zelfs naar de analyse van het probleem.

Als je net een opdracht hebt gekregen, komen er meteen verschillende ideeën in je op over hoe je dat aan zou kunnen pakken. Als de opdracht bijvoorbeeld is om een kluisdeur te ontwerpen, denk je direct aan de kluisdeuren die je in films gezien hebt, daarbij zien we pinnen die in de muur schuiven en vaak een combinatieslot met verschillende draaischijven. Misschien denk je ook wel aan de kluisdeuren van Harry Potter, met grote wielen waaraan gedraaid moet worden om de kluis te openen en een draak om deze te bewaken.

Oplossingen die je al eerder gezien hebt, en al ervaring mee hebt, is een logische beginstap voor een ontwerp. Dit kan echter ook een valkuil zijn. Als we altijd beginnen bij de ontwerpen die al gedaan zijn, zullen we nooit echte grote verbeteringen ontwerpen. Daarnaast slaan we hiermee eigenlijk een stap uit de cyclus van Figuur 2 over. In plaats van het probleem eerst uitgebreid te analyseren en daarmee op een passende set criteria te komen, gaan we direct naar de synthese en bedenken we voorlopige (deel)ontwerpen op basis van onze ervaring.

Begin bij de basisprincipes

Dat het beginnen bij oplossingen die je al eerder gezien hebt een probleem kan zijn werd ook benoemd door Elon Musk in de video van Figuur 1. Als hij alleen naar de beschikbare accu’s en accutechnologieën had gekeken, was hij vermoedelijk tot de conclusie gekomen dat een betaalbare elektrische auto niet mogelijk was. In plaats daarvan keek hij naar de basiscomponenten van deze accu’s. Zo kon hij inzien dat het mogelijk zou moeten zijn om de accu’s voor elektrische auto’s een stuk betaalbaarder te maken. Zo zien we dat redeneren vanuit de basisprincipes je helpt om vooruit te kijken en om oplossingen te onderzoeken die nu nog niet bestaan. Dat is precies waar ontwerpen over gaat.

In de video heeft Elon Musk het vooral over de kosten van de accu’s waar hij naar kijkt. Dat is begrijpelijk voor een ondernemer. Als werktuigbouwkundig ontwerpers hebben wij ook wel met kosten te maken, maar is de technische uitdaging vaak belangrijker. Daarom zullen wij voornamelijk naar de fysische principes achter de opdracht kijken. We identificeren wat de belangrijkste natuurkundige verschijnselen waar we in het ontwerp mee te maken zullen krijgen, en bepalen welke grootheden daarbij horen. Door die grootheden met elkaar in verband te brengen krijgen we al een gevoel voor wat er belangrijk is aan het ontwerp en waar de grootste uitdagingen zitten.

Het redeneren vanuit de fysische principes is hiermee een belangrijk onderdeel van de probleemanalyse. Door de juiste grootheden te identificeren, en hier waarden aan toe te kennen, kan je de criteria van het ontwerp goed specificeren en ook meetbaar maken. Later in het ontwerpproces helpt dit bij het beoordelen van de concepten en natuurlijk ook bij het verkopen van je ontwerp aan de opdrachtgever.

Hoe doe je dat dan?

Een probleem analyseren bij de fysische basisprincipes klinkt heel mooi, maar hoe ziet dat er in praktijk uit? Vaak start je bij de projectbeschrijving. Daar vind je al randvoorwaarden en specificaties die je iets vertellen over wat het ontwerp moet doen en kunnen. Denk hierbij aan de manier waarop het ontwerp van energie voorzien wordt (netspanning, batterijen, zwaartekracht, …), omstandigheden waaronder het ontwerp gebruikt zal worden (trillingen, temperatuur, druk, …) of verplichte onderdelen (plaatstaal, veren voor aandrijving, …).

Een andere nuttige techniek om de basisprincipes te achterhalen is een “filmpje” maken van het verwachte functioneren van het ontwerp. Wat moet het ontwerp doen, welke bewegingen horen daarbij? Vaak is het nuttig om tijdens deze beweging de energie-omzettingen in kaart te brengen. Wat voor energie gaat het ontwerp in en hoe wordt deze energie gebruikt tijdens het verwachte functioneren?

Om nog wat duidelijker te maken hoe je dit kan doen, en wat het resultaat van deze methode kan zijn, voeren we hieronder een analyse uit voor de opdracht van WOP2 in 2023.

Voorbeeld: VertiGO Car

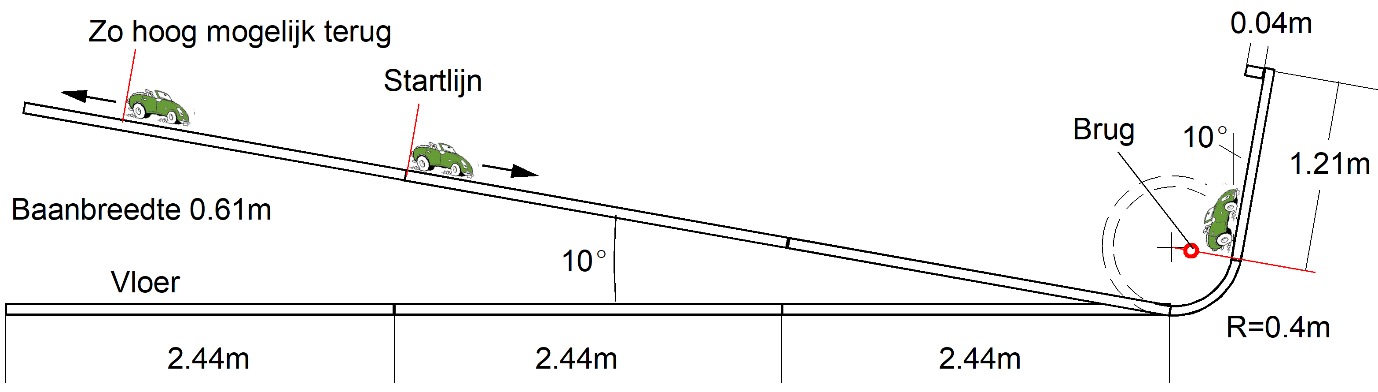
In 2023 was de WOP2 opdracht om een wagentje te ontwerpen die vanuit stilstand in beweging kwam, over een steil stuk baan omhoog reed en vervolgens zo hoog mogelijk terug de baan op reed. Hierbij waren de volgende ontwerpuitdagingen in de opdracht gegeven:

1. Ontwerpen van de V‐Car met aandrijving.
2. Helling af rijden / regeneratie van energie voor het omkeerpunt 1)
3. Maximaliseren van de terugweg.
4. Minimaliseren van energieverlies tijdens rijden.
5. Rechtuit rijden.

Voor het construeren van het wagentje was er plaatmetaal beschikbaar. Daarnaast werden er skatewielen met een diameter van 76 mm gegeven aan de groepen en konden de groepen kiezen uit een vaste set veren voor de aandrijving.

Welke Fysische Principes zijn belangrijk?

Laten we de opdracht eens vanuit de natuurkundige principes bestuderen. Wat is er eigenlijk belangrijk?

Aannames

In dit proces zullen we verschillende aannames maken. Die zullen we expliciet maken door ze op deze manier naast de tekst te plaatsen.

Om een goede score te halen, moeten we in ieder geval zo ver mogelijk terug rijden de baan op. Het lijkt dus belangrijk om goed te specificeren hoe ver we terug kunnen en willen rijden.

Om op dit punt te komen, is er voldoende energie nodig om de hele baan af te leggen. Deze energie komt uit de hoogte van het wagentje bij de start, en uit de veer die het wagentje aandrijft. Voor de veer kunnen we nog een keuze maken uit zes verschillende types. Mogelijk kunnen we aan de hand van energie al een eerste selectie maken.

Een grote beperkende factor in ons ontwerp, zal de wrijving zijn. Hierdoor verliezen we namelijk energie, die daardoor niet meer nuttig gebruikt kan worden.

Tenslotte is ook de wrijving tussen de wielen en de baan belangrijk. Wanneer de aandrijfkracht van de wielen op de baan groter wordt dan de maximale wrijvingskracht zullen deze namelijk gaan slippen. Als dat gebeurt kunnen we in korte tijd veel van de energie die opgeslagen is in de veer kwijt raken. Dit moeten we voorkomen.

De uiteindelijke hoogte van het wagentje

Een van de eerste dingen waar we naar kunnen kijken, is wat we moeten doen om een zo hoog mogelijke score te halen. Dat doen we door zo ver mogelijk de baan terug op te rijden. De uiteindelijke hoogte van het wagentje bepaalt onze score.

We gaan op zoek naar een geschikte manier om hier een waarde aan te geven. We zien in de tekening dat de baan horizontaal 7,32 meter lang is en een helling van 10 graden heeft. Hieruit volgt dat de uiteindelijke hoogte van ons wagentje 1,29 meter zal zijn.

Aanname

We nemen (natuurlijk) aan dat we de hoogst mogelijke score willen halen. Daarom gaan we er vanuit dat ons wagentje tot het einde van de baan terug rijdt.

Vaak is het handig om met energie te rekenen. Laten we daarom de uiteindelijke hoogte van het wagentje ook uitdrukken in de hoogte-energie die daarbij hoort. Deze is

\[ E_{h,eind} = mgh = 20 \cdot 1{,}29 = 25{,}8\,\text{J} \]

Aanname

In de afgelopen jaren zagen we dat de wagentjes een massa van ongeveer 2kg hadden. Daarom nemen we hier \(mg=20\,\frac{\text{kg}\cdot\text{m}}{\text{s}^2}\)

De energie aan de start

Aan het begin heeft het wagentje ook al hoogte-energie die gebruikt kan worden. Wanneer het wagentje naar beneden rolt, zal deze energie namelijk omgezet worden in bewegingsenergie. De beginhoogte van het wagentje is 0,86 meter en dus

\[ E_{h,start} = 20\cdot 0.86 = 17{,}2\,\text{J}.\]

Dat betekent dus dat we minstens \(8{,}6\,\text{J}\) aan energie uit de veer moeten halen om het einde van de baan te kunnen halen. In praktijk zal dit zelfs nog een stuk meer zijn omdat we ook rekening moeten houden met wrijving.

De energie van de veer

Voor dit project waren er zes verschillende veren, allemaal afkomstig van Alcomex, beschikbaar. De gegevens van de beschikbare trekveren staan hieronder in Tabel 1, de gegevens van de drukveren in Tabel 2 en de gegevens van de torsieveren in Tabel 3. Een groot deel van de gegevens in deze tabellen komt direct van de leverancier, maar sommige waarden, waaronder de maximaal opgeslagen energie in de veren, hebben we zelf moeten berekenen. Voor het berekenen van de energie hebben we telkens het oppervlak onder de kracht-weg grafiek (of moment-hoek grafiek voor de torsieveren) bepaald.

Tabel 1: Gegevens van de beschikbare trekveren, afgeleid van de brochure van Alcomex, massa bepaald uit 1 meting

Type	\(L_0\) (mm)	\(f_n\) (mm)	\(F_n\) (N)	\(c\) (N/mm)	\(F_0\) (N)	\(E_\text{max}\) (J)	\(m\) (g)
T1590	136	251	87	0,24	23,8	14,3	68
T1940	139	222	157	0,60	23,8	20,1	126

Tabel 2: Gegevens van de beschikbare drukveren, afgeleid van de brochure van Alcomex, massa bepaald uit 1 meting

Type	\(L_0\) (mm)	\(L_n\) (mm)	\(F_n\) (N)	\(c\) (N/mm)	\(E_\text{max}\) (J)	\(m\) (g)
D2790	200	55,6	158,87	1,10	11,5	32
D3130	240	70,8	233,40	1,38	19,7	60

Tabel 3: Gegevens van de beschikbare Torsieveren, afgeleid van de brochure van Alcomex, massa bepaald uit 1 meting

Type	\(\alpha (^\circ)\)	\(M\) (Nmm)	\(c\) (Nmm/\(^\circ\))	\(E_\text{max}\) (J)1	\(m\) (g)
TOR2070	142	2914	20,6	7,2	90
TOR2250	308	2914	9,50	15,6	172

¹ Energie en massa is berekend voor een set van twee torsieveren

Als we kijken naar de energieën die we in deze veren op kunnen slaan, valt direct op dat de torsieveren van type TOR2070 nooit genoeg energie kunnen bevatten om de maximale hoogte te bereiken. Voor trek- en drukveren T1590 en D2790 geldt dat hier op zich genoeg energie in past, maar dat de marge vrij beperkt is. Hieruit kunnen we nu al concluderen dat deze types veren afvallen voor ons ontwerp.

Slip in de wielen

Wanneer de aandrijfkracht te hoog is, kunnen de wielen gaan slippen en verliezen we alle opgeslagen energie in de veer. Hoe veel koppel kunnen we op de as zetten zodat er net geen slip optreedt?

De normaalkracht die werkt op elk van de wielen wordt gegeven door

\[ F_n = \frac{1}{4} \cdot 20 = 5\,\text{N}.\]

Aanname

We nemen, voor nu, aan dat het wagentje vier wielen heeft en dat het gewicht van het wagentje evenredig over de vier wielen verdeeld zal worden.

De maximale wrijvingskracht is dan

\[ F_\text{w,max} = \mu\cdot F_n = 4\,\text{N}.\]

Aanname

We nemen aan dat de skatewielen een wrijvingscoëfficiënt hebben van 0,8 met de houten baan. Die waarde ligt dicht bij de waarde voor rubber op asfalt en is in de afgelopen jaren een redelijke schatting gebleken.

Gegeven dat de wielen een diameter van 76 millimeter hebben, kunnen we het maximale aandrijfkoppel berekenen.

\[ M_\text{max} = F_\text{w,max}\cdot r = 0{,}152\,\text{Nm}.\]

Hieraan zien we meteen dat het niet mogelijk zal zijn om de torsieveren direct op de as te bevestigen. Deze hebben een koppel van ongeveer 3 Newtonmeter, wat 20 keer te groot is.

Voor de trek- en drukveren zal er altijd een overbrenging naar de as gemaakt moeten worden. De eenvoudigste vorm de we kunnen verzinnen is een touwtje direct dat direct om de as gedraaid wordt. Wat zou dan het aandrijfkoppel zijn?

\[ M_\text{T1940} = F_n\cdot r_\text{as} = 0{,}393\,\text{Nm}\] \[ M_\text{D3130} = F_n\cdot r_\text{as} = 0{,}700\,\text{Nm}\]

Dit laat al direct zien dat ook voor deze veren en verbindingsmethode er altijd slip zal optreden wanneer de veer volledig gespannen is. Het moment is hier respectievelijk 2,6 en 4,6 keer te groot. Hieruit concluderen we dat er een transmissie nodig zal zijn.

Conclusies en resultaten

Uit deze verkenning hebben we een aantal conclusies kunnen trekken:

• Bij het beoordelen van onze ideeën moeten we op de opgeslagen energie, verliezen door wrijving en slip letten
• Er is een energiebijdrage van minstens 8,6 Joule nodig vanuit de veer om op de terugweg het einde van de baan te halen
• Alleen de veren met types T1940, D3130 en TOR2250 zijn hiervoor geschikt
• We zullen altijd een transmissie nodig hebben om slip te voorkomen, mits we natuurlijk de aangeleverde wielen voor de aandrijving gebruiken.

Deze conclusies krijgen in de volgende stap een plek in ons programma van eisen en in de morfologische kaart. Het voorkomen van slip, en dus het omlaag brengen van de aandrijfkracht, is een functionele eis. De minimale energieopslag van 8,6 Joule in de veren komt in het PvE als een randvoorwaarde, en door de veren te onderzoeken hebben we de rij “Energieopslag” in onze morfologische kaart al teruggebracht van 6 naar 3 opties.

Zijn we nu klaar?

Nee!

Het onderzoeken van de fysische principes achter je ontwerp is een doorlopend proces. We hebben nu een eerste analyse gedaan zodat we geïnformeerd kunnen beginnen met het ontwerpen van ons karretje, maar ook later in het ontwerpproces is het nuttig om je af te vragen welke onderliggende principes er achter je oplossing zitten.

Sowieso is ontwerpen een cyclisch proces. Je zult dus waarschijnlijk terug komen in een analyse fase op een later moment van het ontwerpproces. Dat is een goed moment om opnieuw te analyseren welke fysische principes relevant zijn in je deelontwerp en/of welke principes onder de problemen die je gevonden hebt liggen.

Daarnaast kan je de fysische basisprincipes gebruiken in de andere fases van het ontwerpproces. Bij het beoordelen van concepten kan het bijvoorbeeld helpen met het ontdekken van nuttige berekeningen om deze te beoordelen. Berekeningen zoals we hier gedaan hebben om te bepalen welke veren geschikt zijn kan je vaak ook doen aan je concepten. Uitvinden welke berekeningen hiervoor geschikt zijn is alleen vaak moeilijk. Als je teruggaat naar de fysische principes achter de oplossingen zie je je ontwerp vaak in een nieuw licht, waardoor de grootheden die je eenvoudig kan berekenen een stuk duidelijker worden.

Referenties

Roozenburg, N. F. M., en J. Eekels. 1998. Productontwerpen, structuur en methoden. 2016 2e dr. Den Haag: Lemma.